Remember when you realized that math wasn’t just numbers? Suddenly letters were involved, too? It’s at that point that you started to learn algebra. Depending on how long ago your memory is drifting back to, you might be rusty on this whole basic algebra thing.
On the SAT Math section, there’s a set of questions called The Heart of Algebra. Essentially, this is all about the fundamentals of algebra. And, at the very beginning of all algebra concepts is linear equations.
Kickstart Your SAT Prep with Test Geek’s Free SAT Study Guide.
What are Linear Equations?
Linear equations make straight lines on graphs.
Makes sense, right? Linear = straight.
The reason linear equations make straight lines when graphed is because they don’t have exponents. No exponents mean we’re always going to have a straight line.

On a real SAT, you’ll likely find 2-4 questions that test how to solve linear equations. They could be:
- Linear equations in one variable – a linear equation that contains one variable (something like x or y)
- Linear equations in two variables – a linear equation that contains two different variables (something like x and y)
- Word problems that involve linear equations
This makes linear equations a frequently tested topic on the SAT. You should be able to identify linear equations and be able to consistently solve linear equations of both one and two variables.
We’ll start with linear equations in one variable.
Linear Equations in One Variable
First, you need to be able to identify linear equations in one variable. This is important because the SAT isn’t going to tell you what skill is required on a particular question. It’s your responsibility to know (a) what type of question you’re working with and (b) how to solve it.
What would 200 EXTRA POINTS do for you? Boost Your SAT Score with Test Geek SAT prep.
How to Identify a Linear Equation in One Variable on the SAT
Linear equations in one variable will contain:
- A single variable
- No exponents
Let’s do a knowledge check
Which of these are linear equations in one variable?
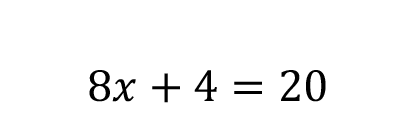 |  | There are no exponents, and we have a single variable (x). |
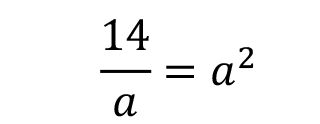 |  | Our variable (a) has an exponent. |
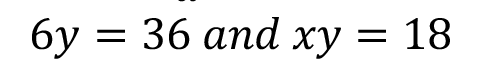 |  | We have two variables (x and y). This is a linear equation in two variables. We’ll get to these later. |
Now that we know how to identify linear equations in one variable, we can talk about how to solve these linear equations.
How to Solve Linear Equations in One Variable
The key to solving linear equations in one variable is isolating the variable. In other words, we want to get our variable all by itself.
Rule: Whenever you do something to one side of an equation, you must do it to the other side as well.
Remember this rule and you’ll be a whiz at linear equations in no time.
Let’s look at an example.
Example 1:
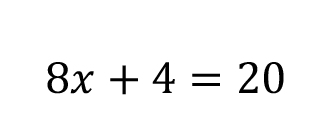
Ask yourself, “how would you isolate x?”
There are several paths you can take here, but I’m always looking for the simplest (and fastest) path on the SAT. Don’t waste any time!
We can start to get x by itself by getting rid of the 4 that’s on the left side. We can subtract this 4 from the left side, but we’ll also need to subtract 4 from the right side. Remember that rule! What you do to one side, you must also do to the other side.
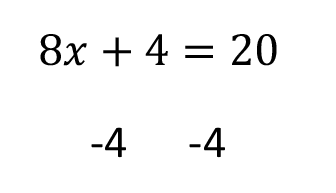
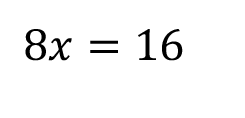
Great! We’re getting closer. Now, we need to get rid of that 8 attached to our x. It’s important to note that when you have a number right next to a variable like that, it’s being multiplied.
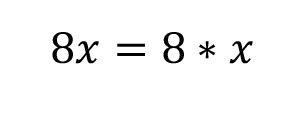
So, if you want to get rid of the 8, we need to divide both sides by 8.
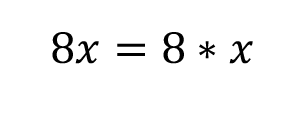
Look at that! We’ve isolated our variable. That’s our answer.
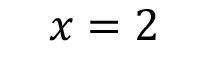
Example 2:
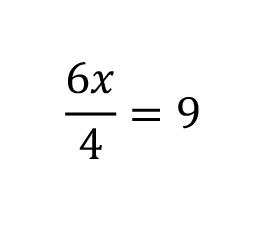
In order to start isolating our variable, we need to get rid of that 4. 6x is being divided by 4. The opposite of division is multiplication. So, we are going to multiply both sides by 4.
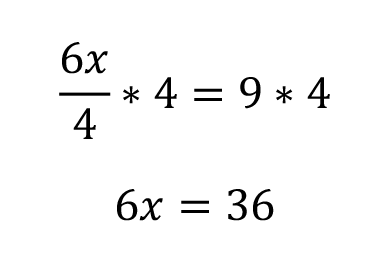
Now it looks like Example 1. To isolate x, we divide both sides by 6.
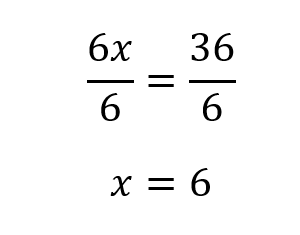
And, we have our answer.
Example 3:
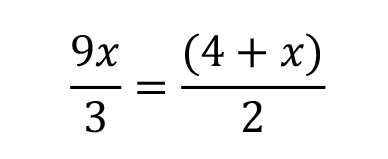
Time for another practice question.
Tip: Any time you see one fraction that is set equal to another fraction, you should be thinking multiply and divide. Or, you may be more familiar with the term cross multiply and divide.
Recall that a fraction is
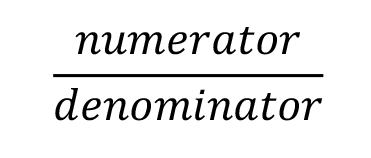
To multiply and divide, use this formula:
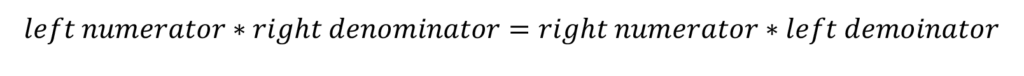
Plug in to the multiply and divide formula.
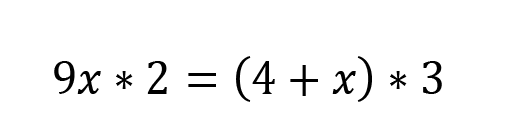
Multiply out to help simplify. To perform multiplication on the right side, you need to distribute that 3 into every term inside the parentheses.
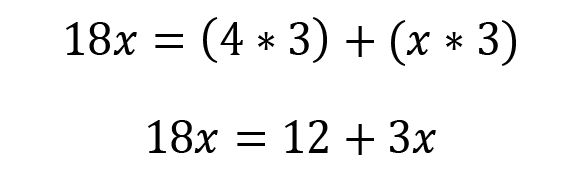
Combine like terms. Subtract the 3x from both sides.
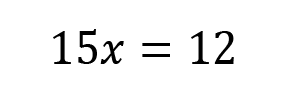
Sometimes SAT linear equation questions won’t be so straightforward, though.
Linear Equation in One Variable – Word Problems
Occasionally SAT linear equation questions are in the form of word problems. I know, I know. Word problems probably aren’t your favorite, but don’t be tempted to just skip these questions because there’s lots to read. They’re actually pretty simple.
When we have a word problem, we need to translate the words into a mathematical equation. Then, we can solve it just like we’ve done previously. Don’t let wordiness on the SAT trip you up.
Example 4:

Rule: “Is” in a word problem can be translated as “=”

Now we need to translate “10 more than 14.” We can think about “more” as “+.”
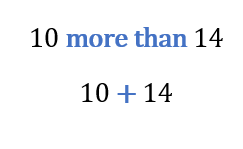
Let’s put it all together.
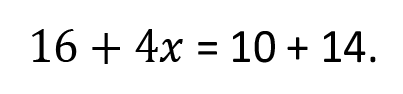
Simplify the right side.
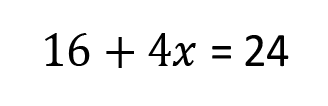
Now it looks just like the simple linear equations we’ve been working with. Let’s isolate that variable.
Start by subtracting 16 from both sides.
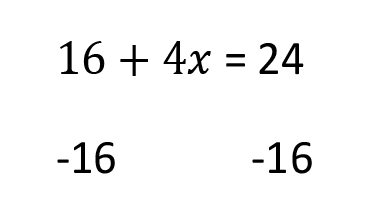
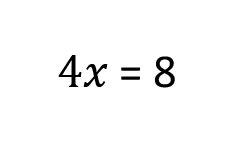
Now we divide both sides by 4.
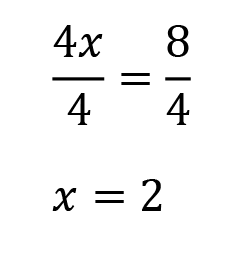
We have our answer! Right? …..right? Nope. We always need to circle back up to the original question and make sure we are truly answering the SAT’s question.
Let’s take a look.

In this case, the SAT is asking us for the value of 8x. So, we need to multiply the x value we found by 8 to get the final answer.
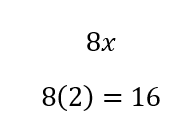
The answer is C.
Example 5:
x + y = 45
The equation above relates the number of minutes, x, Eli spends running each day and the number of minutes, y, he spends skateboarding each day. In the equation, what does the number 45 represent?
A) The number of minutes spent running each day
B) The number of minutes spent skateboarding each day
C) The total number of minutes spent running and skateboarding each day
D) The number of minutes spent skateboarding for each minute spent running
This question is testing your understanding of the relationship between a real-word concept and algebraic expression. We need to reason through what the equation represents in order to solve this correctly.
What would 200 EXTRA POINTS do for you? Boost Your SAT Score with Test Geek SAT prep.
If x represents the number of minutes spent running and y represents the number of minutes spent skateboarding, and we add those two numbers together what do we get? We should get the total number of minutes Eli spent doing these two things. This makes our answer C.

Linear Equations in Two Variables
Let’s move on to linear equations in two variables. Linear equations in two variables have multiple variables.
Rule: We need one distinct equation for each variable.
If we have two variables (x and y), we need two equations in order to solve for x and y. If we have three variables (ex. a, b, c), we need three equations in order to solve for a, b and c.
How to Identify a Linear Equation in Two Variables on the SAT
Check if both are true:
- More than one variable
- No variables have exponents.
Let’s do a knowledge check.
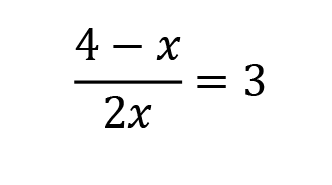 |  | Contains only one variable. Even though the variable x shows up twice, it’s still the same variable, so it counts as one. |
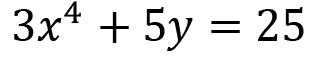 |  | Contains a variable with an exponent. |
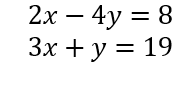 |  | Contains more than one variable and the variables don’t have exponents. |
How to Solve Linear Equations in Two Variables: 2 Methods
There are two main ways to solve linear equations in two variables:
- Substitution
- Elimination
Typically, both methods are possible, but usually only one is optimal. One method may be much quicker than the other. That should be your goal: to quickly assess which method will get you to the answer more quickly. It’s important you understand how to use both methods, so you can choose the best one for the given question.
Substitution Method
The process for using substitution to solve linear equations is 4 basic steps:
- Identify an equation to start with. (You choose which equation)
- Solve the chosen equation for one of the variables. (You choose which variable)
- Plug in to your second equation to find variable #1.
- Plug variable #1 in to either equation to solve for variable #2.
It’ll make more sense as we walk through an example.
Example 6:
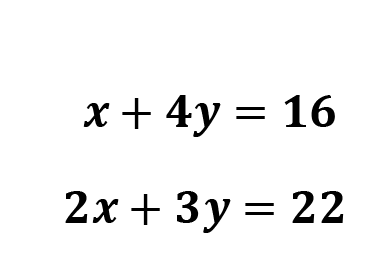
- Identify an equation to start with.
You can choose whichever equation you’d like. You’ll get the same results either way, but the goal is to make this as easy as possible, so I’m going to choose the first equation. I notice that the first equation has a variable, x, that doesn’t have a coefficient, so this will make it very easy to work with
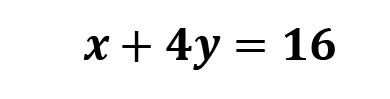
2. Solve the chosen equation for one of the variables. (You choose which variable)
I could solve for y here, but it would be a little messier since I would have to do division. Because the x doesn’t have any coefficient, it’ll be easier to solve for x.
Subtract 4y from both sides.
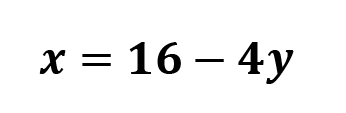
3. Plug in to your second equation to find variable #1.
Now, we can plug in 16 -4y wherever we see x in our second equation.
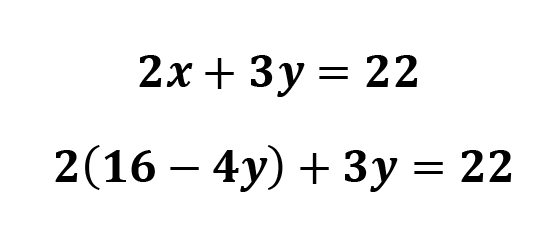
Multiply out the left side.
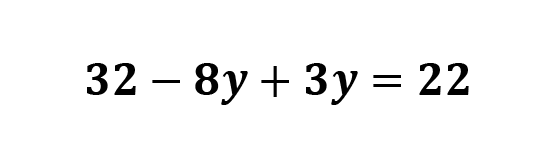
We’re working with a single variable linear equation now, so use the methods I shared in the single variable linear equation section to isolate the variable y.
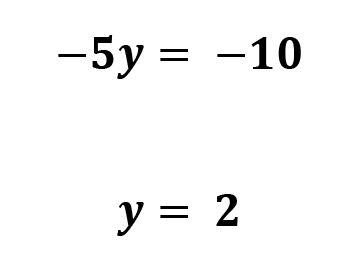
4. Plug variable #1 in to either equation to solve for variable #2.
You can plug y= 2 into either equation to solve for x. Focus on choosing the one that will be quicker. In this case, I think it’ll be quicker to plug into the first equation.
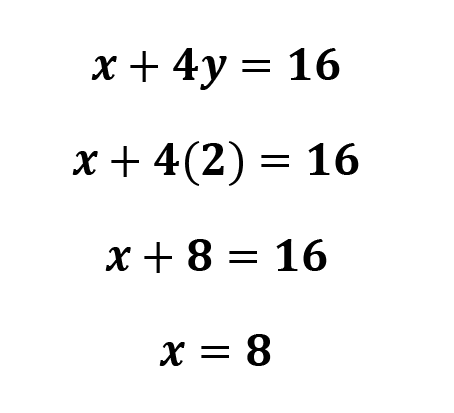
Elimination Method
Sometimes elimination will be the quicker path to solve a system of linear equations. As you do more practice, you’ll start to see patterns that will help you make the decision.
The process for using elimination is three steps:
- Choose a variable to eliminate. Perform any multiplication or division needed.
- Add or subtract the equations to remove one of the variables and solve for the other variable.
- Plug in to solve for the remaining variable.
Let’s walk through an example.
Example 7:
Solve for x and y.
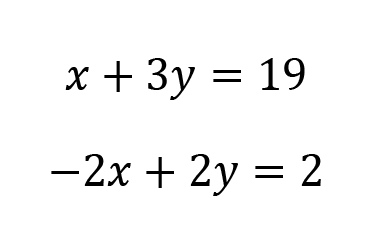
- Choose a variable to eliminate. Perform any multiplication or division needed.
The trick here is to identify the variable that will be easy to eliminate. To eliminate a variable, we need the coefficients to be opposite. For example, -4a and 4a would cancel out. Or 3x and -3x would also work.
When I look at this system of equations, I notice that the x variables are already opposite in sign. The first equation has a positive x and the second has a negative x. So, it’d be pretty simple for me to multiply the first equation by 2 to get a pair that would cancel out (be eliminated) in my next step.
Feeling Overwhelmed? Get 1-on-1 SAT Help from a Test Geek Tutor.
Let’s multiply the first equation by 2. Remember, what we do to one side, we must do to the other, so we’re going to multiply the left and right side by 2.
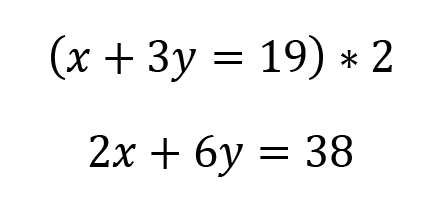
2. Add or subtract the equations to remove one of the variables and solve for the other variable.
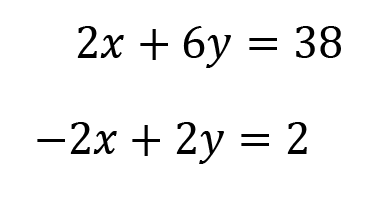
Because of what we did in step 1, we can now add these two equations together and our x variables will be eliminated.
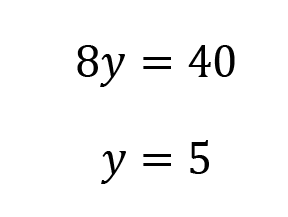
3. Plug in to solve for the remaining variable.
We can choose either equation to plug in y=5. Choose the one that will be quicker to solve. I’ll use the first equation.
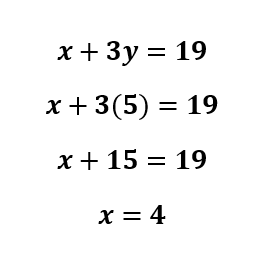
It’s important to note here that this system of equations could have been solved with either elimination or substitution. Focus on asking yourself which method will be quicker, or which method will require less steps to get to the end solution. The more practice you do, the easier it will be to determine which method works better.
Let’s work through some practice questions.
Example 8:
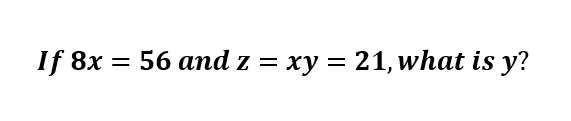
We know this is a multi-variable linear equation because we have, you guessed it, multiple variables and none of our variables have exponents. We must have two distinct equations (which we do in this case) because we have two variables: x and y.
First step is to determine if we should use elimination or substitution.
In this case, substitution will be the better option because our first equation can quickly be solved for x. Then, we can plug it in to our second equation and solve for y.
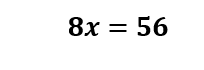
Divide both sides by 8.
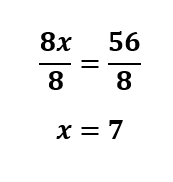
Plug in x=7 to xy=21.
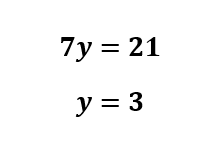
Try another practice question.

Notice this question has 3 variables and 3 equations. Substitution is going to make the most sense, because, like Example 5, one equation only has one variable. We can start there and then move forward with substitution.
Solve for z.
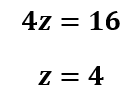
Plug z into the second equation.

One more variable to solve for. Let’s use the final equation to solve for x by plugging in y=1.

Nice work. Let’s do one final practice question.
Example 9:
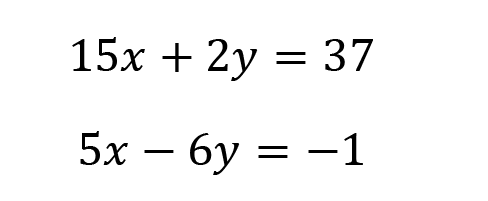
This is a great candidate for elimination. If we multiply the second equation by -3, we could eliminate 15x and -15x.
Multiply the second equation by -3.
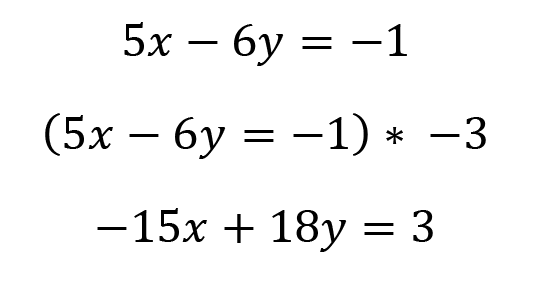
Add the equations together, eliminating x.
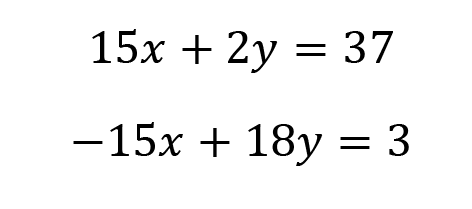
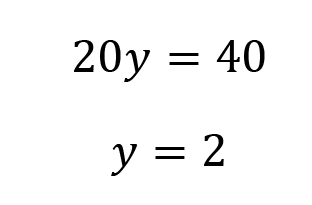
Plug y=2 into either equation to solve for x. I’ll use the second equation.
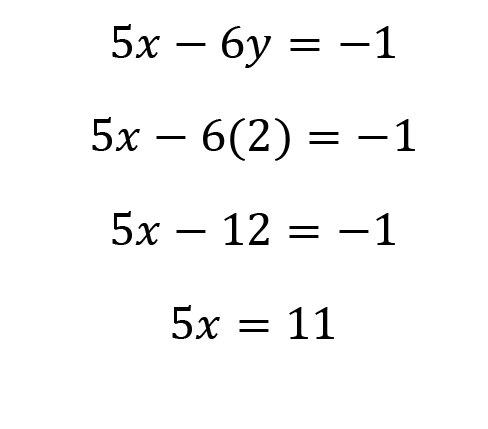
Divide by 5, and we have our answer.
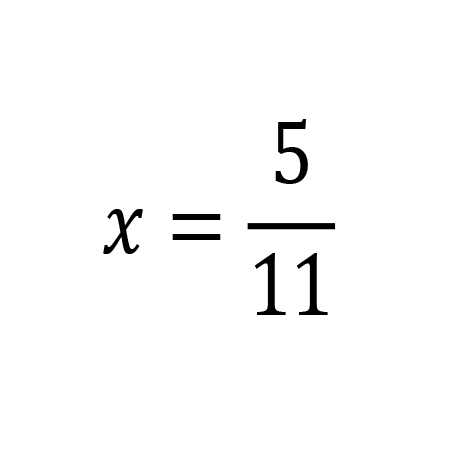
Final Thoughts
Solving linear equations is a must-know skill for the SAT Math section. Understanding how to identify linear equations in both one and two variables is the first steps to success. From there, you should use the methods I’ve laid out to solve.









Comments