What do you get when you multiply a leprechaun by a unicorn? What about a mermaid times a centaur? And what does any of this have to do with SAT math?
Imaginary things exist in math. For example, what is the square root of -1? Surely there is such a number — we can of course imagine it — but what is it? The square of any real number is a positive number (1*1=1 and -1*-1=1), so it can’t be a real number. Instead, just like unicorns and leprechauns and mermaids and centaurs, this number is imaginary.
Kickstart Your SAT Prep with Test Geek’s Free SAT Study Guide.

Imaginary vs. Complex Numbers
First, let’s make a small distinction. Imaginary and complex numbers are not exactly the same thing:
- Imaginary Numbers don’t appear on the number line. One example is the square root of -1 discussed above. We can call this number i.
- Complex numbers are the sum of a real number and an imaginary number. 5+i is an example of a complex number.
The Imaginary I
Being good at imaginary and complex numbers on the SAT math section really comes down to being good at handling i. Remember:
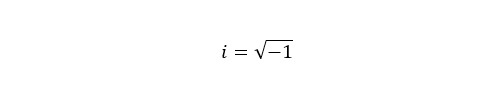
This designation allows us to do all of our normal mathematical operations on the square root of -1, even if we don’t have an actual number for it.
Just as we could with any radical, we can square it:
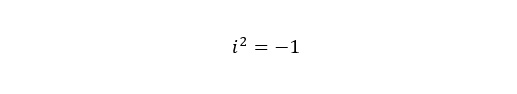
We can cube it:
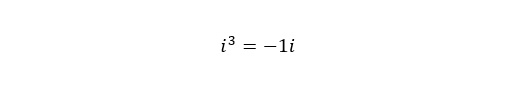
How did we end up with that? Because it is really just this:
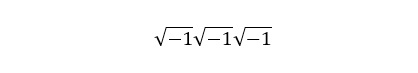
We can raise i to any power we wish, and we can combine radicals like normal:
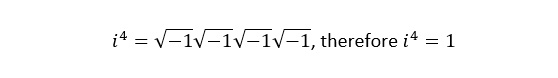
Therefore, our goal when we see a problem with i in it is to make our way to real numbers as much as possible. Square what you can square, cancel what you can cancel and get rid of i as much as possible.
Feeling Overwhelmed? Get 1-on-1 SAT Help from a Test Geek Tutor
Complex Numbers: Mixing the Imaginary with the Real
Complex numbers are the sum (addition) of an imaginary i and a real number. It’s sort of like if I told you I’m part man and part centaur. I might look fast and majestic to you, but just imagine what my centaur half can do.
Complex numbers, in their most basic form, look like this:
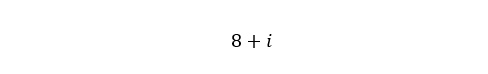
But we can also get pretty fancy, and we all know the SAT math section likes to get fancy:

How Complex and Imaginary Numbers are Tested on the SAT Math Section
There are two basic types of complex number questions on the SAT math section:
- Combine stuff problems
- Fancier problems
Yes, I know the technical jargon can be confusing.
The first type of question will simply ask you to try to get rid of i, or at a minimum, simplify and get rid of some instances of i.
Here’s an example:

FOILing will get us where we need to go:

The second type is the fancy stuff. We will need to do more than just combine terms to get these questions correct, but the good news is that the SAT tends to return to the same trick time and time again: equivalencies.
Let’s take a look:

Our first step is to multiply both the top and bottom of the original equation by the conjugate of the denominator. This simply means that we are flipping the middle sign in the denominator and then going where the math leads us:

Looking at our answer choices, we can see that a quick split of our two terms yields option C. That’s it — smoother than a chinchilla on a velvet slide.

How Frequently are Imaginary and Complex Numbers Tested?
I like to analyze the official SAT practice tests that College Board has released. I think we can learn a lot by examining what College Board views as their “canonical” practice tests. In looking at tests 1-10, I found that complex and imaginary numbers were tested five times:
Test 1, Section 3, Problem 2
Test 2, Section 3, Problem 11
Test 4, Section 3, Problem 14
Test 6, Section 3, Problem 3
Test 7, Section 3, Problem 4
Want a convenient resource for these practice tests, along with answers and explanations? Check out our FREE SAT PREP GUIDE.
What can we learn from this analysis? Three things:
- You have about a 50-50 shot at seeing one of these problems. That makes them less common than topics like linear equations but more common than topics like the discriminant.
- You’ll probably only see complex number problems in section three. A calculator would be a huge advantage with these problems because most calculators can handle i. Therefore, College Board is probably only going to throw them at you in section three.
- These problems can range from very easy (problems 2, 3 and 4) to hard (problems 11 and 14). This reflects the two ways of testing these concepts (combining stuff vs. fancier problems).
Final Thoughts on Complex and Imaginary Numbers
In a lot of ways, getting better at the SAT math section is sort of like making a massive checklist of everything you might need to know and then moving through the list methodically until you are a master of everything. Truthfully, many of the concepts aren’t that hard.
Complex and imaginary numbers aren’t hard. They’re just weird. We are used to thinking of numbers as existing somewhere on the number line, but imaginary numbers don’t live there. Fortunately, they can be manipulated with the same tools that we use to manipulate regular radicals and variables, so the actual math we are doing in these problems should be familiar to you.
Oh, and when you multiply a leprechaun by a unicorn? You get Lucky Charms. Come on, people.









Comments