If you want to maximize your SAT Math score, you need to improve two things:
- Your ability to do math from pre-Algebra, Algebra 1, Algebra 2, and occasionally Geometry and Trigonometry
- Your critical reasoning skills
That second one – critical reasoning skills – is why a lot of students who are good math students in school don’t do as well as they think they will on the SAT Math sections. You might be used to seeing math concepts tested in a pretty straightforward way at school. Well…buckle up because the SAT doesn’t really do straightforward. This test is really good at making hard questions out of easy math.
Kickstart Your SAT Prep with Test Geek’s Free SAT Study Guide.
Maximizing Your SAT Math Score – The Heart of Algebra
It’s important to brush up on all of your math concepts, but it’s equally important to do a lot of real SAT math practice questions, so you get used to the type of questions you’ll see on test day and improve those reasoning skills!
Top scores don’t just happen from cramming all the math you’ve ever learned. The fact is, the College Board, who creates the SAT, has a lot of documentation on exactly what is “fair game” to be tested. (Don’t worry, we’ll get to this list of of “fair game” topics down below.)
Maybe you’re reading this and you have a few years before you need to buckle down and get serious about taking the SAT, but most likely, the SAT test date is set and you have weeks or maybe a few months to prepare.
Think of this as your study guide for the Heart of Algebra section of SAT Math.
SAT Math Sections
Let’s back up for a second. The SAT has two math sections: Section 3 and Section 4 of the test.
- Section 3: 20 questions (15 multiple choice, 5 open response), 25 minutes, no calculator
- Section 4: 38 questions (30 multiple choice, 8 open response), 55 minutes, calculator
These two sections include questions that fall into four categories as defined by the SAT’s College Board:
- Heart of Algebra (30%)
- Problem Solving & Data Analysis (30%)
- Passport to Advanced Math (30%)
- Additional Topics (10%)
The Heart of Algebra makes up 30% of the math questions you’ll see on the SAT. That works out to 19 questions total – including both multiple choice and open response.

As you work through the two Math Sections, you’ll notice that the questions start getting more difficult. This is normal. This is also true for both the multiple choice and the open response questions, and, this pattern repeats itself on Section 4.
You’ll find questions that fall into the Heart of Algebra category throughout both Math sections. Easier Heart of Algebra questions will be at the beginning, and as you progress through the rest of the multiple choice, you’ll start seeing more difficult questions. It’s all about the complexity of the question – not just the core concept that’s tested. Remember – the SAT is really good at making hard questions out of easy math.
What would 200 EXTRA POINTS do for you? Boost Your SAT Score with Test Geek SAT prep.
It can be helpful to consider this pattern and consider how you pace yourself throughout the Math sections. You may need more time per question towards the end of the math sections.
SAT Heart of Algebra
In this guide, we’re going to look at the Heart of Algebra category of questions. The Heart of Algebra focuses on topics you likely covered in Pre-Algebra or Algebra 1. As you move through the other core math topic areas, you get to more advanced math topics. In the SAT Heart of Algebra section you’ll find questions testing your understanding of:
It may have been a while since you’ve solved linear equations. Maybe you’re a little rusty? Not to worry! Let’s start by understanding more specifically what you need to be able to do to score well on Heart of Algebra questions.
SAT Heart of Algebra: 7 Things You Need to Know
1. [Linear Equations] Solve, simplify, or interpret linear expressions or equations in one variable. Linear equations look something like this:
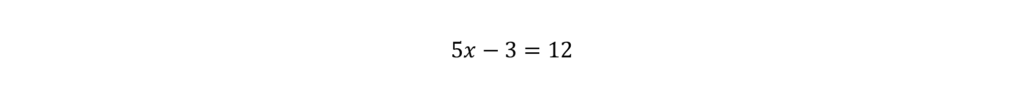
Notice that I also said linear expressions. Expressions and equations are very similar, but expressions won’t have an equals sign. So, on the SAT, you may see an expression like this:
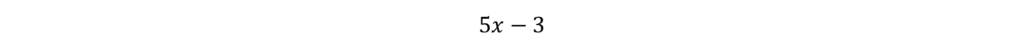
In one variable simply means the expression or equation contains only one variable. In the examples above, that variable is x. Expressions or equations you work with on the SAT may require multiple steps in order to simplify or solve for the variable. They could be pretty straightforward, or more complex, multi-step problems.
If you’re asked to solve a linear equation, the equation may have no solution, one solution or infinitely many solutions.
2. [Linear Inequalities] Solve, simplify, or interpret linear inequalities in one variable. Linear inequalities look something like this:
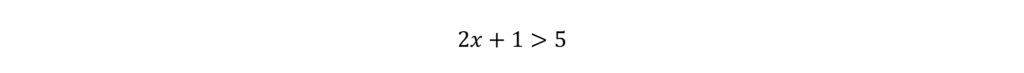
One side does not equal the other. Instead of an equal sign (=), we have greater than (>) or less than (<) signs to work with. While linear equations give us one distinct answer like x = 5, linear inequalities give us a range of where our answer can be found.
Again, multiple steps may be required on the SAT in order to simplify or solve for the variable in these inequalities.
3. [Linear Equations] Create a linear function that models a linear relationship between two things. Moving on from expressions and equations, we arrive at functions.
These types of questions may involve using two variables or function notation to model the relationship described in the question. A function looks something like this:
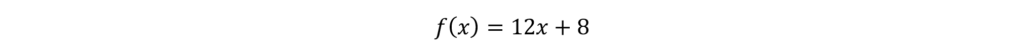
A function describes a relationship – a relationship between x and f(x). You can plug in any value of x into a function and get a result. This result is your f(x). For the SAT, you need to fundamentally understand how functions can be used and how to come up with a function based on given information about a relationship between two things.
4. [Linear Equations] Solve, simplify, or interpret linear equations in two variables. This is just like #1, except now we are dealing with two variables. You need to be able to analyze a system of linear equations and understand the constraints between two variables.
If you’re asked to solve a system of linear equations, the system may have no solution, one solution or infinitely many solutions.
5. [Linear Inequalities] Solve, simplify, or interpret linear inequalities in two variables. This is just like #2, except now we are dealing with two variables. You need to be able to work with an inequality that contains two variables as well a systems of inequalities.
6. [Linear Equations] Understand the relationship between a particular context (i.e. real-world scenario) and linear functions. These are those dreaded word problems. You’ll need to be able to make connections between the real-world context and the linear equation that models the context. You may be asked for the meaning of a constant term, a variable, or a feature of an equation.
7. [Graphing Linear Equations] Understand connections between algebraic and graphical representations of linear equations. You’ll need to be able to:
- Select a graph described by a given linear equation.
- Select a linear equation that describes a given graph.
- Determine the equation of a line given a description of its graph.
- Determine features of a graph of a linear function based on its equation.
- Determine how a graph would be affected by a change in its equation.
If you want to maximize your SAT Math score, make sure you understand – and have practiced – questions that fall under each of the above seven sub-categories in the Heart of Algebra section.
We’ve covered the general topics you should know within the Heart of Algebra on the SAT Math, but now let’s take a look in more detail at each of main areas: linear equations, linear inequalities, and graphing linear equations.
Some of this may be a review for you. Use this guide however is helpful for you. That may be skimming and double checking your understanding of the concepts we’ll cover, or it may be deep-diving into each topic. Let’s start with linear equations.

Linear Equations
Linear equations are the foundation of Algebra 1. When you start learning algebra and introducing variables into math, you start with linear equations. That’s because they are simple. They contain one variable and, when graphed, you get a straight line.
The reason linear equations make straight lines when graphed is because they don’t have exponents. No exponents mean we’re always going to have a straight line.
On a real SAT, you’ll likely find 2-4 questions that test how to solve linear equations. They could be:
- Linear equations in one variable – a linear equation that contains one variable (something like x or y)
- Linear equations in two variables – a linear equation that contains two different variables (something like x and y)
- Word problems that involve linear equations
This makes linear equations a frequently tested topic on the SAT. You should be able to identify linear equations and be able to consistently solve linear equations of both one and two variables.
We’ll start with linear equations in one variable.
Linear Equations in One Variable
The key to solving linear equations in one variable is isolating the variable. In other words, we want to get our variable all by itself.
Rule: Whenever you do something to one side of an equation, you must do it to the other side as well.
This rule is really important, especially as you tackle more complex linear equation questions. You don’t want to make simple mistakes on these questions.
Let’s look at an example.
Example 1:
If 6(x+2) -4 = 14, what is the value of x?
Ask yourself, “how would you isolate x?”
There are several paths you can take here, but I’m always looking for the simplest (and fastest) path on the SAT. Don’t waste any time!
Answer:
Start by adding 4 to both sides. Then, multiply out that 6 to both terms inside of the parentheses.
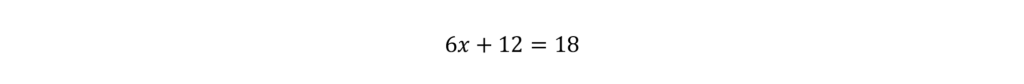
Great! We’re getting closer. Now, let’s subtract the 12 from both sides.
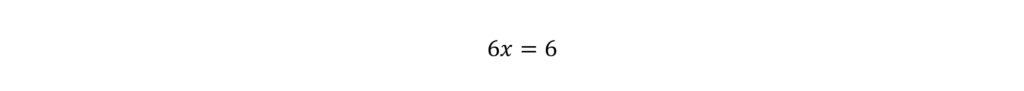
Divide both sides by 6.
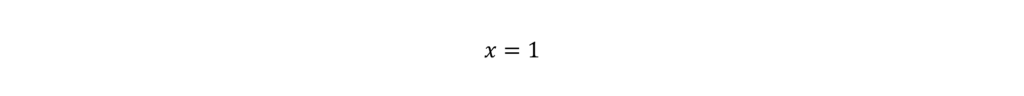
Example 2:
So far, we’ve been talking about equations, but the SAT does sometimes test expressions as well. The difference here is that expressions are groups of numbers and variables, but they do not contain an equals sign. Let’s go over an example.

In this question, we aren’t solving for x. We are asked which answer choice is equivalent to our given expression. In other words, which answer choice is equal to the given expression. It may not always be obvious where to start with these types of questions, but one option is to try to move some things around in your given expression and see if you start getting close to your answer choices.
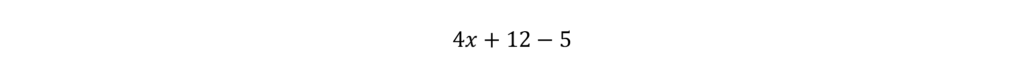
Simplify if you can. In this case, combine 12 and -5
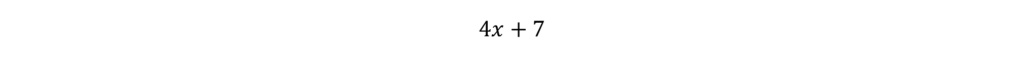
Does this match an answer choice? Yep!

Linear Equations in Two Variables
Let’s move on to linear equations in two variables. If we have two variables (x and y), we need two equations in order to solve for x and y. If we have three variables (ex. a, b, c), we need three equations in order to solve for a, b and c.
You’ll see this concept tested in the form of systems of linear equations. Let’s look at an example.
Example 3:
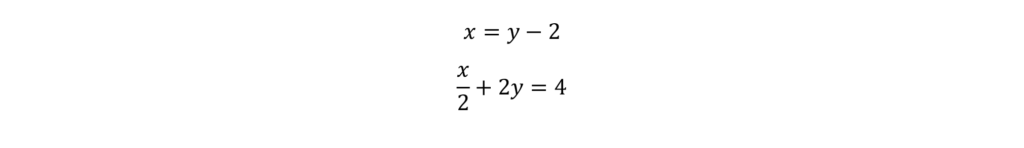

There are two main ways to approach this question.
Approach 1:
Plug in your answer choices into the system of equations. This is a good approach if you feel stuck. It may be more time consuming than Approach 2, but it can certainly work!
Tips:
- Use the simpler equation to test your answer choices. In this case, the first equation is simpler, so try to use that one first and see if you can eliminate any answer choices. The correct ordered pair must work for both equations in the system.
- Start with answer choices that will be easy to plug in. Plugging in 0 usually helps you eliminate terms (and thus simplifying your work). This can help you quickly rule out answer choices and avoid unnecessary work.
Start with A and plug in (-2, -2). x = -2, y = -2.
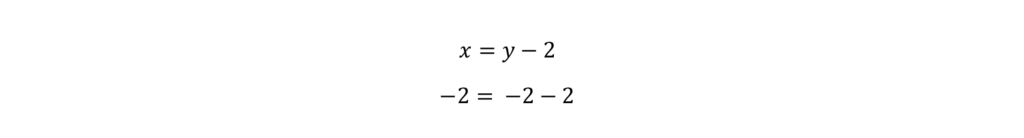
-2 does not equal -4
We can eliminate A.
Try B and plug in (4, -2). x = 4, y = -2
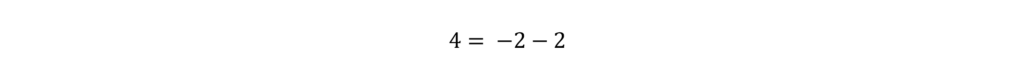
4 does not equal -4
We can eliminate B.
Try C and plug in (0, 2). x = 0, y = 2
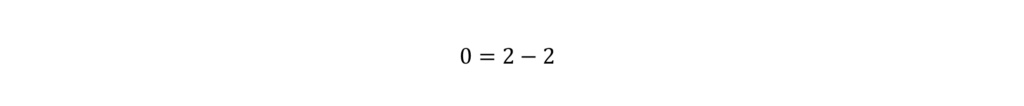
Yes! 0 = 0.
It can be tempting to go with C and move on to the next question, but we have a bit more work to do. It’s possible that C only works for the first equation, so we need to test it on the second equation.
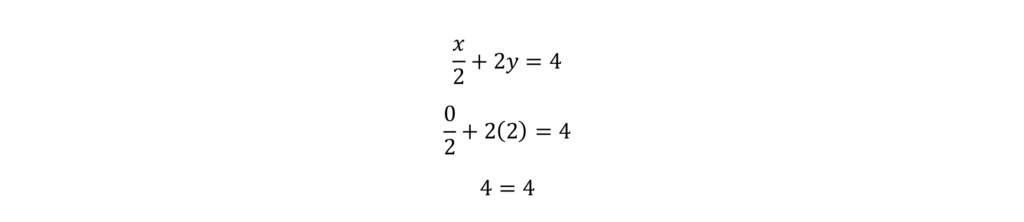
Awesome. Now we have our answer! If you are unsure, you can always test your remaining answer choices as well.
Approach 2:
Instead of plugging in answer choices you can use either elimination or substitution to solve for x and y. In this case, substitution method works better. We actually already have x isolated in the first equation. Plug y – 2 in for x in the second equation and solve.
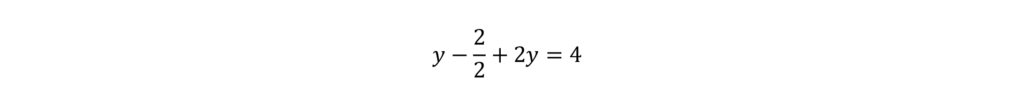
To get rid of the fraction, multiply everything by 2.
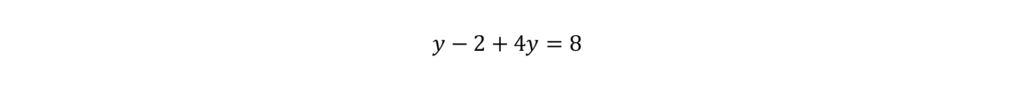
Combine like terms.
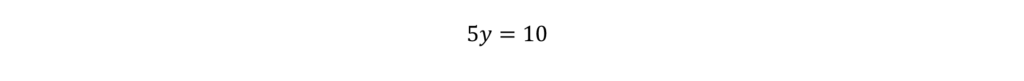
Divide by 5.
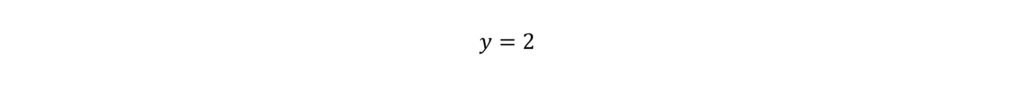
In this case we only have one answer choice with y = 2, so we have found our answer: C.
Linear Inequalities
Have you ever thought about what the term “inequality” means? Inequality literally means “not equal,” and that’s exactly what’s going on with mathematical linear inequalities. One side does not equal the other. Instead of an equal sign (=), we have greater than (>) or less than (<) signs to work with.
Feeling Overwhelmed? Get 1-on-1 SAT Help from a Test Geek Tutor.
While linear equations give us one distinct answer like x = 5, linear inequalities give us a range of where our answer can be found.
To be able to solve linear inequalities on the SAT, you need to know the following inequality signs:


Linear Inequalities in One Variable
For the most part, you can treat linear inequalities just like linear equations. Key word is most. So, what’s the exception? If we divide or multiply by a negative number, we have to flip the sign of the inequality.
Rule: Flip the sign when you multiply or divide by a negative number.
Let’s look at an example.
Example 4:

First, we should recognize this as a linear inequality equation because of the inequality sign (>) rather than an equal sign.
We’re going to solve this just as we would solve a linear equation question: isolate x.

Add 3 to both sides.

Divide by 5.

We’ve solved the linear inequality, but now we need to return back to our question and see what it’s asking for.

It asks for a possible value. Because we are dealing with an inequality, x could be any number in a range of values, and the SAT wants us to identify which answer choice is in that range.
Think to yourself: if x has to be greater than 2, what is one possible value that x could be? Any number that is greater than 2, so… 3, 4, or 5.
At this point you would take a look at your answer choices and determine which one is greater than 2. Our answer will be D.
Nicely done.
Linear Inequalities in Two Variables
Example 5:
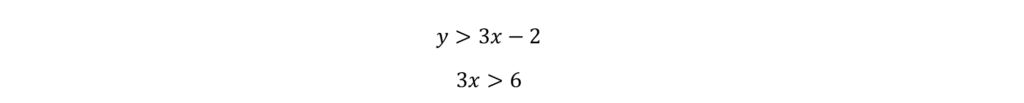

This is a bit of a tricky question. It relies on your reasoning ability more than your ability to solve straightforward linear inequalities.
You may notice that there’s a repeated expression (or part of an expression) in both inequalities. In the first inequality, we have 3x – 2 and in the second one, we have 3x. This is a good thing to notice. If we can get these two expressions to be exactly equivalent, we can get to our answer. How? Let’s look at this another way.
What if the question said:
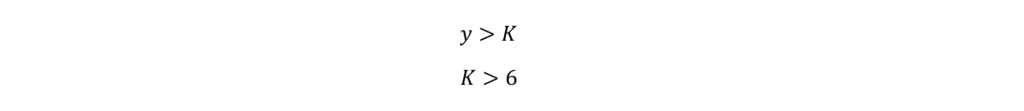
What would be the range of values of y that would satisfy the system of equations?
If y > K and K > 6, then it stands to reason that y > 6. This is relying on your logical reasoning skills. The more practice you do, the better you’ll get at recognizing these kinds of things.
Alright – now going back the question as it is written, you may start to see why I might want the 3x and 3x – 2 to be exactly equivalent. I want to be able to do the kind of logic I was able to do with our magical variable K above.
What can we do to 3x to make it equivalent to 3x – 2? Subtract 2. If we subtract 2 from one side, we must also subtract 2 from the other side. So our second inequality becomes:
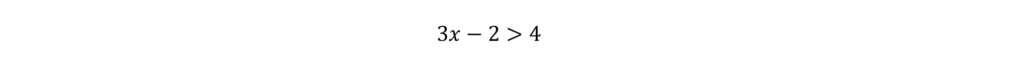
So, following our logic, we can say that y > 4. And, we have our answer: B.
Graphing Linear Equations
SAT graphing linear equation questions are all about using the y = mx + b formula. Look familiar? y = mx + b is the slope intercept form of a line. Remember: all linear equations, when graphed, are straight lines!
Let’s break down this formula.
In the slope intercept form of a line, m is the slope. The slope is how much a line rises or falls as it moves from left to right. In other words, slope is a measure of how steep a line is and if it’s going up (positive) or down (negative). Mathematically, slope can be represented as:
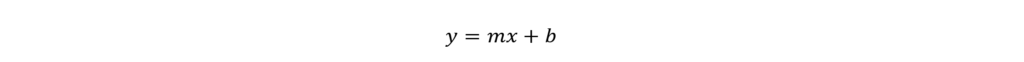
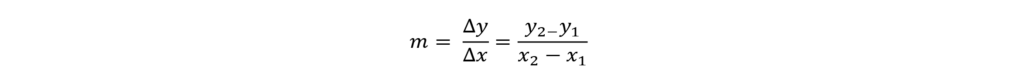
If we know any two points, we can calculate the slope of a line. As you get more comfortable with how expressions relate to their graphs, you’ll start to see how the slope of two lines can tell us about how the two lines are related. For the SAT, it’s important to know:
- Two lines that are parallel have the same slope.
- If line a is perpendicular to line b, line a’s slope will be the negative reciprocal of line b’s slope.
In the slope intercept form of a line, b is the y-intercept. The y-intercept of a line is where the line crosses the y-axis. We’ve already learned how to make use of the y-intercept by translating it into a point.
The y-intercept, b, is a constant – just like the slope, m. While b and m can never change for a given line, we can infinite x and y values on that line.
The SAT wants to test your reasoning skills and how you navigate using this formula given various combinations of information to start with. It’s good to know that:
- If you have any two points or a single point plus b, you can solve for slope.
- If you know slope and you know b, you can solve for x if you have y.
- If you know slope and you know b, you can solve for y if you have x.
The point is: you need to identify what exactly you do have when you start a problem, so you know how to work towards what you don’t have.
What would 200 EXTRA POINTS do for you? Boost Your SAT Score with Test Geek SAT prep.

How to Use y = mx + b
Now that you understand what the m and b are in the slope intercept form of a line, y=mx+b, let’s look at how to make use of this on the SAT.
y = mx + b only works if the y is by itself, and thus, has a coefficient of 1. This is really important. If your line isn’t in correct form, you’re going to get the wrong answer.
Let’s look at an example.
Example 6:
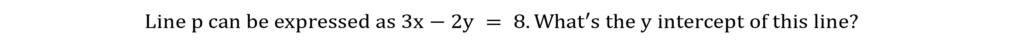
First things first. We need to get this line into the normal y=mx+b form. In order to do this, we want to isolate y.
Let’s subtract 3x from both sides.
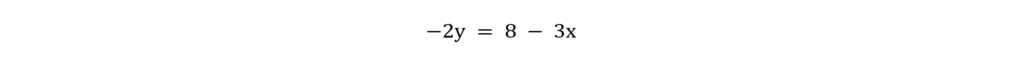
Divide by -2.
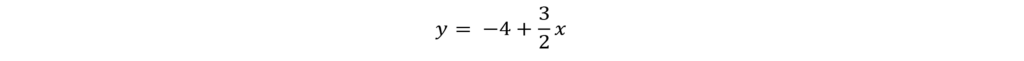
We’re really close. It’s always a good idea to get into the exact form of y = mx + b, so you don’t make any simple mistakes. We can do this by moving things around on the right side.
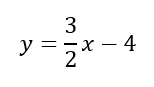
Great! Now we can see that our y intercept (b) is -4.
Read This if You’re Short on Time
Trying to cram everything you need to know to ace the Heart of Algebra questions on the SAT Math sections? This is the tl;dr version if you’re short on time.
Linear equations have one or more variables, none of which have exponents.
- Goal: Isolate the variable or variables. (whatever you’re asked to solve for)
- Rule: Whenever you do something to one side of an equation, you must do it to the other side as well.
- Tip: When solving a system of equations (more than one linear equation), use one of the following methods:
- Plug in answer choices
- Substitution – solve for one variable and then plug that variable in to the other equation to get the second variable.
- Elimination – Line up both equations and perform addition or subtraction to eliminate one variable. You can perform some multiplication or division on one or more of the equations first to ensure you can actually eliminate a variable.
Linear inequalities have greater than (>) or less than (<) signs instead of an equals sign. While linear equations give us one distinct answer like x = 5, linear inequalities give us a range of where our answer can be found.
- Goal: Isolate the variable or variables and determine the range of values that a variable could be.
- Rule: Whenever you do something to one side of an equation, you must do it to the other side as well.
- Rule: If you multiply or divide by a negative number, flip the sign.
- Memorize:

Goal:
- Identify a graph based on a given linear equation
- Identify a linear equation based on a given graph
- Use the slope intercept form of a line to solve for slope, y-intercept, or a point on the line.
Memorize:
Slope intercept form of a line, where m is slope and b is the y-intercept.
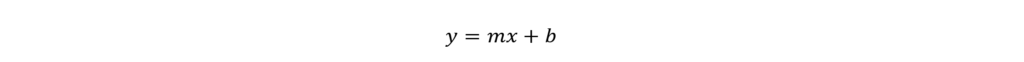
Formula for slope, given two points:
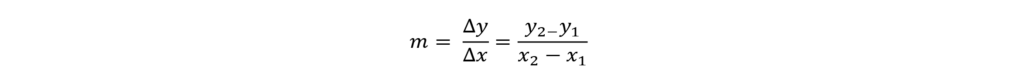
Final Thoughts on SAT Math Heart of Algebra
You can do this. You can get better at these questions. It takes consistent practice, but it is possible! If you’ve worked through everything here, I recommend you download some official SAT practice tests and start practicing!











Comments